多层感知机

文章中不对代码部分做详细介绍

本章节中撰写的代码都放在了 GitHub 开源仓库 中

1 MLP 简介

这一部分的内容在李宏毅的课程有所涉及

mlp 的输出结果是一个类别（例如 0/1, +1/-1），相比较之下，linear 输出的是实数，softmax 输出的是概率

单层的感知机是不可以实现 XOR 的分类的，所以要使用多层感知机， $ \sigma$ 代表激活函数

$$ \mathbf{h}^{(l)} = \sigma\left( W^{(l)} \mathbf{h}^{(l-1)} + \mathbf{b}^{(l)} \right) $$

1.1 隐藏层

隐藏层不可以是线性的，因为多层的线性都可使用一个线性层代表，所以我们要应用非线性函数（称为激活函数）

常见的激活函数有以下几种：

1. Sigmoid: $\sigma(x)=\frac{1}{1+e^{-x}}$
2. Tanh: $\tanh(x)=\frac{e^x - e^{-x}}{e^x + e^{-x}}$
3. ReLU (Rectified Linear Unit): $\text{ReLU}(x)=\max(0,x)$
4. PReLU (Parametric ~): $f(x)= \begin{cases} x, & x \ge 0 \\ a x, & x < 0 \end{cases}$

其中 ReLU 相对常用，并且计算非常的快，前两个容易梯度消失

1.2 输出层

在多类分类中，我们需要将输出层的数量更改到分类的数量，所以使用 softmax 来作为输出层，如下图所示

1.3 参数初始化

在 from scratch 中我们可以注意到 参数中的 W 需要初始化为随机

W1 = nn.Parameter(torch.randn(num_input, num_hidden, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hidden, requires_grad=True))

W2 = nn.Parameter(torch.randn(num_hidden, num_output, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_output, requires_grad=True))

如果 W 全是 0 代表隐藏层所有神经元的输出完全相同，从而梯度也完全相同，训练无法有效进行，所有的神经元的参数和运算完全相同，等同于只有一个神经元

2 模型选择与拟合

2.1 训练误差与泛化误差

• 训练误差：模型在训练集上的误差（例如模拟考）
• 泛化误差：模型在新数据上的误差（例如真正的高考）

所以我们要区分 val 和 test 的数据集， val 是用来评估模型好坏的数据集，但是 test 数据集是只使用一次的数据集

test 是不可以用来对模型的决策做出任何的执导的，不论是超参数还是什么的，不然会导致数据指标的虚高

val 的数据是用来取模型的超参数的，在不是很大的数据集上可以用 K fold

2.2 K fold 交叉验证

k 一般取 5 或者 10 左右的数据

有时候会发现数据集并没有这么大，就会使用这个方法

把数据分成 k 块，每一次训练都选一个作为 val，这样就会拿到 k 个 val 的值，然后取平均数来评估误差

2.3 拟合

模型容量\数据	数据简单	数据复杂
容量低	正常	欠拟合
容量高	过拟合	正常

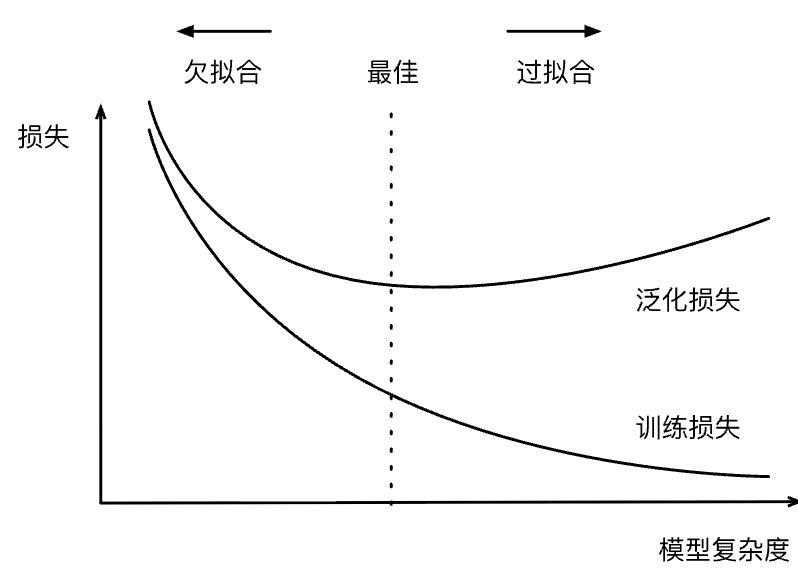
决定模型的复杂度主要有两个点：模型的参数数量和参数可以选择的范围

3 权重衰退

3.1 均方范数

通过限制参数值的选择范围来实现控制模型容量，达到抗过拟合的效果，也被称为 $L_2$ 正则化

通过 范数来进行硬性限制可以直接硬性限制数据选取

$$ \min_{\mathbf{w},\, b}\ \ell(\mathbf{w}, b) \quad \text{subject to} \quad \|\mathbf{w}\|^{2} \le \theta $$

更多是使用柔性的限制（实际上效果是相同的）使用 $\lambda$ 来控制正则的强度，越小则约束越小

$$ \min_{\mathbf{w},\, b}\ \ell(\mathbf{w}, b) + \frac{\lambda}{2}\|\mathbf{w}\|^{2} $$

这就限制了权重系数的选择范围，实际求出来的梯度如下所示

$$ \frac{\partial}{\partial \mathbf{w}} \left( \ell(\mathbf{w}, b) + \frac{\lambda}{2}\|\mathbf{w}\|^{2} \right) = \frac{\partial \ell(\mathbf{w}, b)}{\partial \mathbf{w}} + \lambda \mathbf{w} $$

将结果代入到梯度更新的公式中，可以得到下式子

$$ \mathbf{w}_{t+1} = (1 - \eta \lambda)\,\mathbf{w}_{t} - \eta\, \frac{\partial \ell(\mathbf{w}_{t}, b_{t})}{\partial \mathbf{w}_{t}} $$

这表明我们将 $\bold {w}_t$ 每一次更新前进行了一次衰减，而梯度更新并没有发生变化

总结而言，权重衰退使用了 $L_2$ 正则项使得模型的参数范围减小，从而实现了控制模型复杂度

3.2 代码实现

代码实现查看项目源代码即可

值得一提的是在 pytorch 的一个用法，手动指定某一个参数，而不是全部应用

# 这个表示对 weight 做 weight_decay 但是 bias 不做
trainer = torch.optim.SGD([
    {"params":net[0].weight, 'weight_decay': wd},
    {"params":net[0].bias}],lr=lr)

4 Dropout

本质是让模型对于噪音有抗性

通过对数据加入噪音，同时也不改变数据的期望

$$ x_i' = \begin{cases} 0, & \text{with probability } p, \\ \dfrac{x_i}{1-p}, & \text{otherwise}. \end{cases} $$

一般来说都作用在隐藏层全连接层的输出，这是只在训练中使用的

dropout 是正则项，只会在训练中应用，在推理的时候，dropout 会直接返回输入

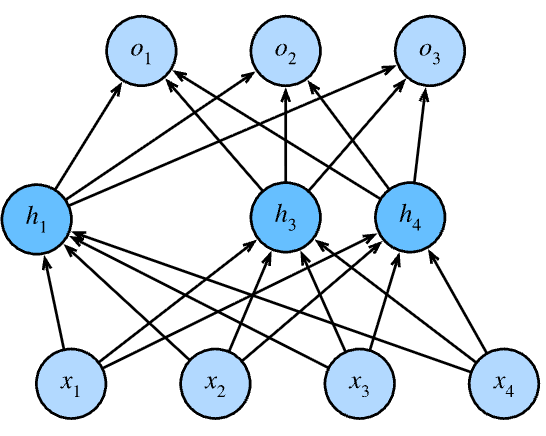
这是一个 dropout 的示例，表示随机将其中一些改成零，另一些放大

一般来说，我们会在每一层分别设置不同的 dropout 概率，越靠近输入层则越应该设置更小的概率

5 数值稳定性

梯度爆炸和梯度消失，为了避免这些情况，我们有可能需要在训练的过程中要调整学习率

ReLU 的导数是 1，会随着数值迅速增大，这很容易导致梯度爆炸，相反 SIGMOD 容易导致梯度消失

梯度消失会导致顶部的训练还算行，但是底部的非常训练效果很差（网络层数很浅）

如何让训练更加稳定，把梯度控制在合理的范围内

1. 把乘法变成加法：ResNet, LSTM
2. 归一化：梯度裁剪和梯度归一化
3. 使用合理的权重或者激活权重

一些常用的知识

inf 一般是梯度过大导致的，而 nan 一般是通过除以 0 来产生的

6 Kaggle 房价预测

这里实现了一个 K 折交叉验证函数，可以注意下

其他的详细代码都放置在了 GitHub 上 上

def get_k_fold_data(k, i, X, y):
    """K 折交叉验证实现, 没有打乱顺序"""
    assert k > 1
    fold_size = X.shape[0] // k
    X_train, y_train = None, None
    for j in range(k):
        idx = slice(j * fold_size, (j + 1) * fold_size) # 创建对应折的 索引序列
        X_part, y_part = X[idx, :], y[idx]  # 拿出对应的实际数据
        if j == i:  # 第 i 折放进 val
            X_val, y_val = X_part, y_part
        elif X_train is None:   # 第一次放进来的时候是空的, 直接赋值
            X_train, y_train = X_part, y_part
        else:   # 用 cat 附加在末尾
            X_train = torch.cat([X_train, X_part], 0)
            y_train = torch.cat([y_train, y_part], 0)
    return X_train, y_train, X_val, y_val